Given
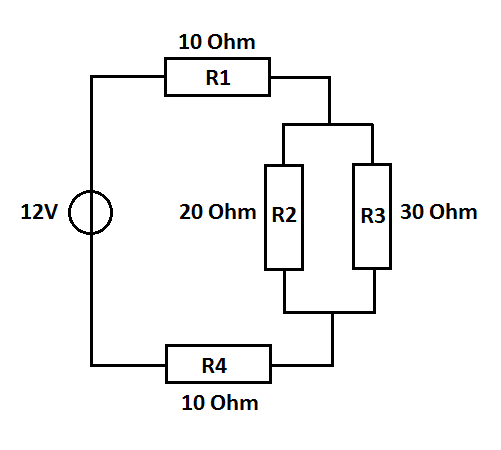
Find
\(R_T; I_T; U_{R_1}; U_{R_{2,3}}; U_{R_4}; I_{R_1}; I_{R_2}; I_{R_3}; I_{R_4}
\)
Solution
\(U_T = 12 V \\
R_T = R_1 + \frac{R_2 * R_3}{R_2 + R_3} + R_4 = 32 \Omega \\
I_T = \frac{U_T}{R_T} = \frac{12 V}{32 \Omega} = 0,375 A \\
\)
Kirchhoff’s voltage law
\(U_T = U_{R_1} + U_{R_{2,3}} + U_{R_4} \\
U_{R_1} = I_T * R_1 = 0,375 A * 10 \Omega = 3,75 V \\
U_{R_{2,3}} = I_T * R_{2,3} = 0,375 A * 12 \Omega = 4,5 V \\
U_{R_4} = I_T * R_4 = 0,375 A * 10 \Omega = 3,75 V \\
\)
Kirchhoff’s current law
\(I_{R_1} = I_{R_2} + I_{R_3} = I_{R_4} \\
I_{R_1} = 0,375 A \\
I_{R_2} = \frac{U_{R_{2,3}}}{R_2} = \frac{4,5 V}{20 \Omega} = 0,225 A \\
I_{R_3} = \frac{U_{R_{2,3}}}{R_3} = \frac{4,5 V}{30 \Omega} = 0,15 A \\
I_{R_4} = 0,375 A \\
\)
Answer
\(R_T = 32 \Omega; I_T = 0,375 A; \\
U_{R_1} = 3,75 V; U_{R_{2,3}} = 4,5 V; U_{R_4} = 3,75 V; \\
I_{R_1} = 0,375 A; I_{R_2} = 0,225 A; I_{R_3} = 0,15 A; I_{R_4} = 0,375 A \\
\)
